Онлайн-расчёты Скачать Статьи-формулы Нормы ОВ Справочник-таблицы Контакты Помощь сайту
Барометрическое давление Вязкость воды Гидравлический расчёт. Метод удельных потерь давления Гидравлический расчёт. Метод характеристик сопротивления Коэффициент пропускной способности Параллельное и последовательное соединение насосов Параллельное и последовательное соединение участков Поведение двухтрубной системы отопления Понятие производной для начинающих Пропускная способность последовательных и параллельных участков Расход воздуха по тепловой мощности Расход воды по тепловой мощности Расчёт расширительного бака Вязкость воздуха Плотность воздуха Скорость потока Температура неотапливаемого пространства Теплотехнические параметры эффективности утилизаторов тепла и холода Тригонометрические функции Эквивалентный диаметр прямоугольного воздуховода Энтальпия воздуха Давление насыщенного водяного пара Парциальное давление водяного пара Относительная влажность воздуха Температура мокрого термометра Принципиальные схемы центральных кондиционеров Единицы измерения теплоты

Поведение двухтрубной системы отопления

Введение

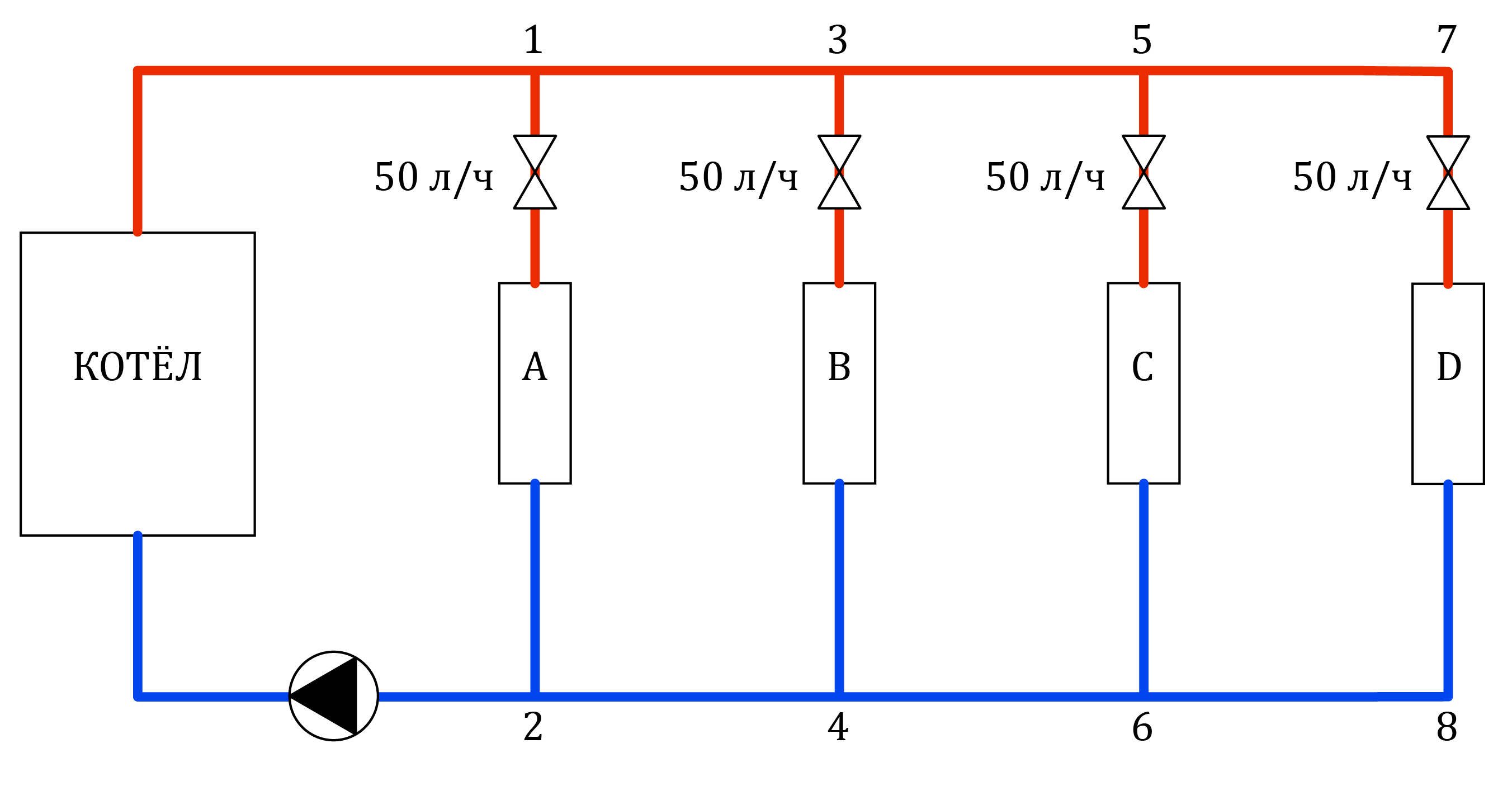
Рассмотрим поведение двухтрубной системы отопления 1↓ в динамическом режиме, то есть когда какие-то клапаны закрываются, а какие-то остаются открытыми. Чтобы увидеть, как поведение системы зависит от характеристик насоса, будет полезно рассмотреть два случая:
  1. если используется насос с постоянной характеристикой
  2. если используется регулируемый насос с поддержанием постоянного давления
Возьмём простую двухтрубную систему отопления из 4х радиаторов и посмотрим, как будет изменяться расход в радиаторах A и B, если перекрыть радиаторы C и D. При параллельном соединении участков эквивалентный расход будет равен сумме расходов в отдельных участках:
$$L_{E}=\sum L_{i} \tag{1}\label{eq:1}$$
\(L_E\) [A]  [A] индекс E означает “equivalent - эквивалентный” - эквивалентный или общий объёмный расход, л/ч или м3/ч (или любые другие единицы объёмного расхода)
\(\sum\) - греческая буква “сигма”, обозначает сумму
\(L_i\) - объёмный расход в каждом из отдельных участков, л/ч или м3/ч (или любые другие единицы объёмного расхода)
Схема
figure Двухтрубная система отопления.png

Общая часть

Скажем также что гидравлические сопротивления Csec [B]  [B] индекс sec означает “section - участок” отдельных участков сети известны, для упрощения возьмём одинаковые сопротивления для участков с радиаторами:
Участок Объёмный расход \(L_{sec}\), л/ч Гидравлическое сопротивление \(C_{sec}\)
2-K-1 200 50 000
1-A-2 50 1 500 000
3-B-4 50 1 500 000
5-C-6 50 1 500 000
7-D-8 50 1 500 000
1-3 150 30 000
3-5 100 30 000
5-7 50 30 000
8-6 50 30 000
6-4 100 30 000
4-2 150 30 000
Зависимость потерь давления \(\Delta p_{E1}\) [C]  [C] индекс 1 означает “режим 1 - все радиаторы открыты” в этой сети от расхода \(L_{E1}\) будет следующая:
$$\Delta p_{E1}=C_{E}\cdot L_{E1}^{2}\tag{2}\label{eq:2}$$  [D]  [D] для переменной L не совсем верно использовать показатель степени 2, так как для прямых участков этот показатель будет в пределах 1.8...1.9. Степень 2 берётся для упрощения расчёта. Подробнее об этом в книге Ганс Роос “Гидравлика систем водяного отопления
графически это парабола
В этой формуле расход \(L_{E1}=200\) л/ч известен, неизвестно эквивалентное сопротивление сети \(C_{E}\). К сожалению не существует формул, с помощью которых можно найти сопротивление сети \(C\), в которой более 2-х параллельно соединённых участков. Поэтому придётся последовательно заменять каждые 2 параллельных участка их эквивалентом и искать эквивалентное сопротивление \(C_{..E..}\). Заменять участки таким образом нужно будет до тех пор, пока сеть не упростится до одного контура. Для того, чтобы найти \(C_{..E..}\)двух участков можно пользоваться такой формулой:
$$C_{..E..}=\frac{C_{1}\cdot C_{2}}{C_{1}+C_{2}+2\cdot\sqrt{C_{1}\cdot C_{2}}} \tag{3}\label{eq:3}$$
Ещё можно найти \(C_{..E..}\) другим способом - используя коэффициент пропусной способности. Чаще коэффициент пропускной способности \(k\) используют как характеристику запорно-регулирующей арматуры - клапанов, фильтов и других и обозначают \(k_{v}\) [E]  [E] индекс v означает “valve - вентиль”, но с его помощью можно также выражать сопротивления труб или фасонных элементов и тогда он обозначается просто буквой \(k\) без индекса. Формула перевода \(C\) в \(k\) такая:
$$k=\sqrt{\frac{10^{5}}{C}}\tag{4}\label{eq:4}$$
и для параллельных участков пропускная способность \(k\) - это просто сумма \(k_{i}\) отдельных участков:
$$k_{E}=\sum k_{i}\tag{5}\label{eq:5}$$
что немного проще, чем формула \eqref{eq:3}
Найдём падение давления \(\Delta p_{sec}\) и пропускную способность \(k_{sec}\), дополним таблицу:
Участок Объёмный расход \(L_{sec}\), л/ч Гидравлическое сопротивление \(C_{sec}\) Падение давления \(\Delta p_{sec}\), Па Коэффициент пропускной способности \(k_{sec}\)
2-K-1 200 50 000
50000⋅0.22 = 2000  [F]   [F]  В формуле используется объёмный расход в м3 ⁄  ч
\(\sqrt{\frac{10^{5}}{C}}=\sqrt{\frac{10^{5}}{50000}}\approx1.41\)
1-A-2 50 1 500 000 1500000⋅0.052 = 3750 \(\sqrt{\frac{10^{5}}{1500000}}\approx0.26\)
3-B-4 50 1 500 000 1500000⋅0.052 = 3750 \(\sqrt{\frac{10^{5}}{1500000}}\approx0.26\)
5-C-6 50 1 500 000 1500000⋅0.052 = 3750 \(\sqrt{\frac{10^{5}}{1500000}}\approx0.26\)
7-D-8 50 1 500 000 1500000⋅0.052 = 3750 \(\sqrt{\frac{10^{5}}{1500000}}\approx0.26\)
1-3 150 30 000 30000⋅0.152 = 675 \(\sqrt{\frac{10^{5}}{30000}}\approx1.83\)
3-5 100 30 000 30000⋅0.102 = 300 \(\sqrt{\frac{10^{5}}{30000}}\approx1.83\)
5-7 50 30 000 30000⋅0.052 = 75 \(\sqrt{\frac{10^{5}}{30000}}\approx1.83\)
8-6 50 30 000 30000⋅0.052 = 75 \(\sqrt{\frac{10^{5}}{30000}}\approx1.83\)
6-4 100 30 000 30000⋅0.102 = 300 \(\sqrt{\frac{10^{5}}{30000}}\approx1.83\)
4-2 150 30 000 30000⋅0.152 = 675 \(\sqrt{\frac{10^{5}}{30000}}\approx1.83\)
Займёмся упрощением сети и поиском эквивалентных сопротивлений :
  1. Параллельно соединённые участки 5-7-D-8-6 и 5-C-6 заменяются эквивалентным 5-ECD-6, находится эвкивалентная пропусная способность \(k_{5ECD6}\)
    Находим гидравлическое сопротивление сопротивление \(C_{57D86}\) последовательно соединённых участков 5-7, 7-D-8 и 8-6:
    $$C_{57D86}=C_{57}+C_{7D8}+C_{86}=30000+1500000+30000=1560000\nonumber$$
    находим \(k_{5ECD6}\):
    $$k_{5ECD6}=k_{57D86}+k_{5C6}=\sqrt{\frac{10^{5}}{C_{57D86}}}+k_{5C6}=\sqrt{\frac{10^{5}}{1560000}}+0.26=0.25+0.26=0.51\nonumber$$
  2. Последовательно соединённые участки 5-ECD-6, 3-5 и 5-4 заменяются эквивалентным 3-ECD-4, находится эквивалентная пропусная способность \(k_{3ECD4}\)
    Гидравлическое сопротивление эквивалентного участка 5-ECD-6 можно найти используя значение пропускной способности \(k_{5ECD6}\):
    $$C_{5ECD6}=\frac{10^{5}}{k_{5ECD6}^{2}}=\frac{10^{5}}{0.51^{2}}=384468\nonumber$$
    если использовать формулу \eqref{eq:3} то сопротивление 5-ECD-6 можно найти так:
    $$\displaylines{C_{5ECD6}=\frac{C_{57D86}\cdot C_{5C6}}{C_{57D86}+C_{5C6}+2\cdot\sqrt{C_{57D86}\cdot C_{5C6}}}=\\=\frac{(30000+1500000+30000)\cdot1500000}{(30000+1500000+30000)+1500000+2\cdot\sqrt{(30000+1500000+30000)\cdot1500000}}=382390\nonumber}$$
    результат различается из-за округления значений \(k\) в меньшую сторону
    тогда \(C_{3ECD4}\)будет:
    $$C_{3ECD4}=C_{35}+C_{5ECD6}+C_{64}=30000+384468+30000=444468\nonumber$$
    $$k_{3ECD4}=\sqrt{\frac{10^{5}}{444468}}=0.47\nonumber$$
  3. Параллельно соединённые участки 3-ECD-4 и 3-B-4 заменяются эквивалентным 3-EBCD-4, находится эквивалентная пропусная способность \(k_{3EBCD4}\)
    $$k_{3EBCD4}=k_{3ECD4}+k_{3B4}=0.47+0.26=0.73\nonumber$$
  4. Последовательно соединённые участки 3-EBCD-4, 1-3 и 4-2 заменяются эквивалентным 1-EBCD-2, находится эквивалентная пропускная способность \(k_{1EBCD2}\):
    $$C_{3EBCD4}=\frac{10^{5}}{k_{3EBCD}^{2}}=\frac{10^{5}}{0.73^{2}}=187652\nonumber$$
    $$C_{1EBCD2}=30000+187652+30000=247652\nonumber$$
    $$k_{1EBCD2}=\sqrt{\frac{10^{5}}{247652}}=0.63\nonumber$$
  5. Параллельно соединённые участки 1-EBCD-2 и 1-A-2 заменяются эквивалентным 1-EABCD-2, находится эквивалентная пропусная способность \(k_{1EABCD2}\)
    $$k_{1EABCD2}=k_{1EBCD2}+k_{1A2}=0.63+0.26=0.89\nonumber$$
  6. Находится эквивалентное гидравлическое сопротивление последовательно соединённых участков 2-КОТЁЛ-1 и 1-EABCD-2 \(C_{E1}=C_{K1EABCD2}\):
    $$\displaylines{C_{E1}=C_{K1EABCD2}=C_{2K1}+C_{1EABCD2}=C_{2K1}+\frac{10^{5}}{k_{1EABCD2}^{2}}\\=50000+\frac{10^{5}}{0.89^{2}}=50000+126247=176247\tag{6}\label{eq:6}}$$

Нерегулируемый насос

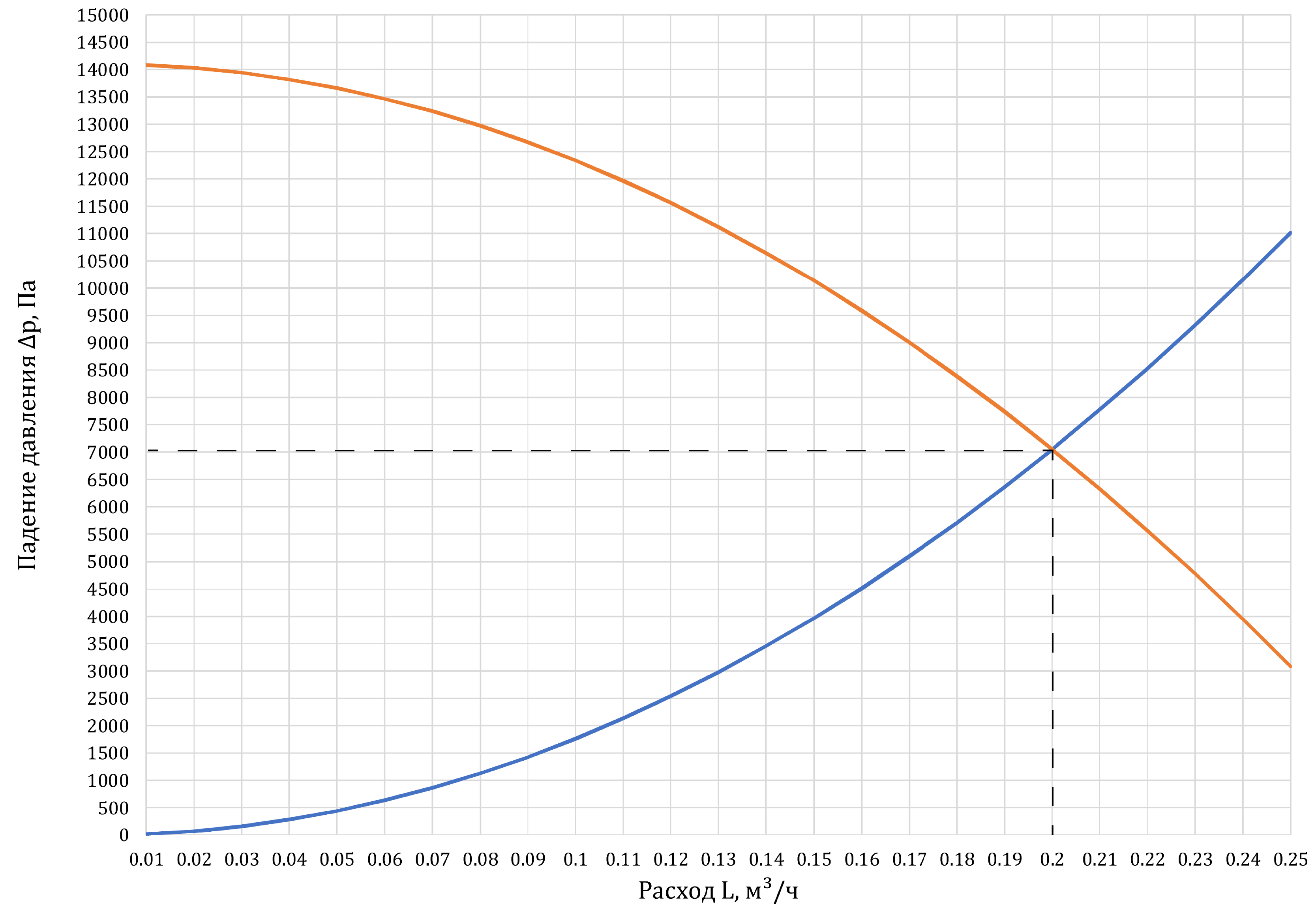
Теперь, зная гидравлическое сопротивление сети \(C_{E1}\) мы можем построить её характиристику 2↓
Характеристика сети при всех открытых радиаторах
figure Двухтрубная система отопления - График 1.png
Посмотрим, как изменится сопротивление системы, если отключить радиаторы C и D
Найдём новое сопротивление \(C_{E2}\)  [G]  [G] индекс 2 означает “режим 2 - часть радиаторов закрыта”, состоящее из \(C_{1EAB2}\) и \(C_{2K1} \) :
$$\displaylines{C_{1EAB2}=\frac{C_{13B42}\cdot C_{1A2}}{C_{13B42}+C_{1A2}+2\cdot\sqrt{C_{13B42}\cdot C_{1A2}}}=\\=\frac{(30000+1500000+30000)\cdot1500000}{(30000+1500000+30000)+1500000+2\cdot\sqrt{(30000+1500000+30000)\cdot1500000}}=382390\nonumber}$$
$$C_{E2}=C_{2K1}+C_{1EAB2}=50000+382390=432390\tag{7}\label{eq:7}$$
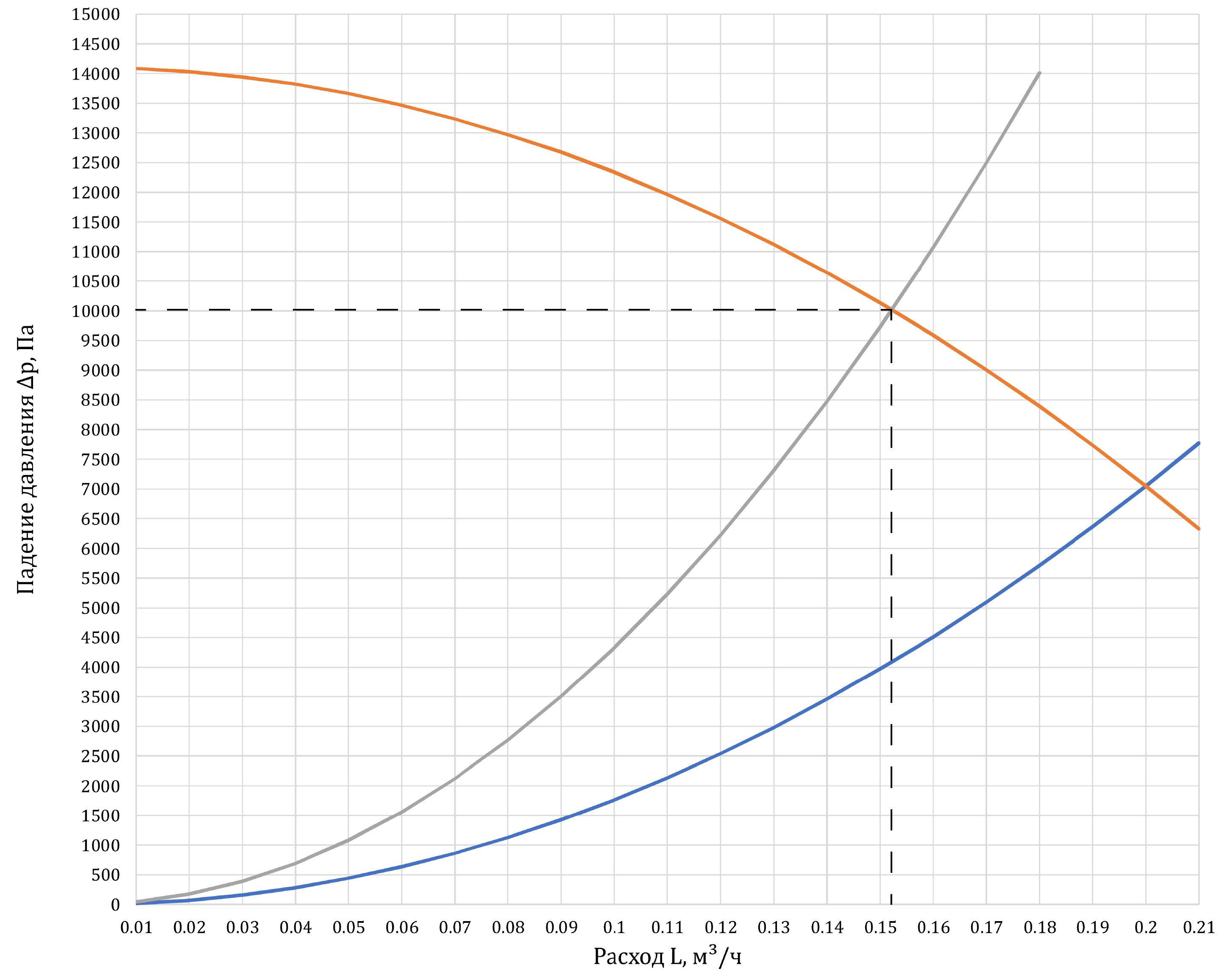
Построим характеристику системы после отключения радиаторов C и D 3↓. Видно, при этой характеристике насоса расход снизится до \(\approx0.152\) м3/ч, а давление, которое развивает насос вырастет до \(\approx 10000\) Па. Так как это всего лишь пример и используется насос с выдуманной характеристикой, точность здесь не слишком важна
Характеристика сети после отключения радиаторов C и D
figure Двухтрубная система отопления - График 2.png
Посмотрим, какой расход воды будет протекать через радиатор A и радиатор B. Сопротивление участка 1-A-2 \(C_{1A2}=1500000\), а участка 1-3-B-4-2 \(C_{13B42}=30000+1500000+30000=1560000\)
Теперь можно найти, как расход распределится по радиаторам A и B, для этого выразим расход \(L_{B}\) через радиатор B через падение давления \(\Delta p_{B}\) и сопротивление \(C_{B}\):
$$L_{B}=\sqrt{\frac{\Delta p_{B}}{C_{B}}}\nonumber$$
Так как новое давление насоса известно - судя по характеристике это \(\approx10000\) Па, можно найти расход в каждом из параллельно соединённых участков. Когда участки соединяются параллельно, падения давлений в них равны, то есть для этого случая \(\Delta p_{1A2}=\Delta p_{13B42}\). Общее падение давления в сети после отключения радиаторов C и D будет складываться из падения давления на участке через КОТЁЛ \(\Delta p_{2K1}\) с новым расходом \(L_{E2}\) и через параллельно соединённые участки с радиаторами A и B:
$$\Delta p_{E2}=\Delta p_{2K1}+\Delta p_{1A2}=\Delta p_{2K1}+\Delta p_{13B42}\nonumber$$
Зная сопротивление участка через КОТЁЛ можно легко узнать значение \(\Delta p_{2K1}\) с новым расходом \(L_{E2}\):
$$\Delta p_{2K1}=C_{2K1}\cdot L_{2K1}^{2}=50000\cdot0.152^{2}=1155\nonumber$$
Падение давления через параллельно соединённые участки с радиаторами можно найти как разность общего давления на сеть и падение давления на участке через КОТЁЛ:
$$\Delta p_{1A2}=\Delta p_{13B42}=\Delta p_{E}-\Delta p_{2K1}=10000-1155=8845\nonumber$$
Так как сопротивление участков 1-A-B и 1-3-B-4-2 разное, расход тоже будет различаться. Найдём расход через радиатор A:
$$L_{1A2}=\sqrt{\frac{\Delta p_{1AB}}{C_{1AB}}=}\sqrt{\frac{8845}{1500000}}\approx0.077\nonumber$$
Тогда расход через радиатор B будет:
$$L_{13B42}=\sqrt{\frac{\Delta p_{13B42}}{C_{13B42}}}=\sqrt{\frac{8845}{1560000}}\approx0.075\nonumber$$
Видно, что расход через радиаторы A и B вырастает где-то в 1.5 раза от расчётного и всё это из-за того, что мы используем нерегулируемый насос с постоянной характеристикой, которая имеет вид дуги. В реальной системе, терморегуляторы радиаторов в итоге отреагируют на повышение температуры в помещении из-за повышенного расхода через радиаторы и скорректируют расход, но было бы лучше, если бы после перекрытия части радиаторов повышения расхода в других вообще не происходило или происходило незначительно. Посмотрим, можно ли этого добиться, если использовать насос, регулируемый по постоянному перепаду давлений.

Регулируемый насос с постоянным перепадом давления

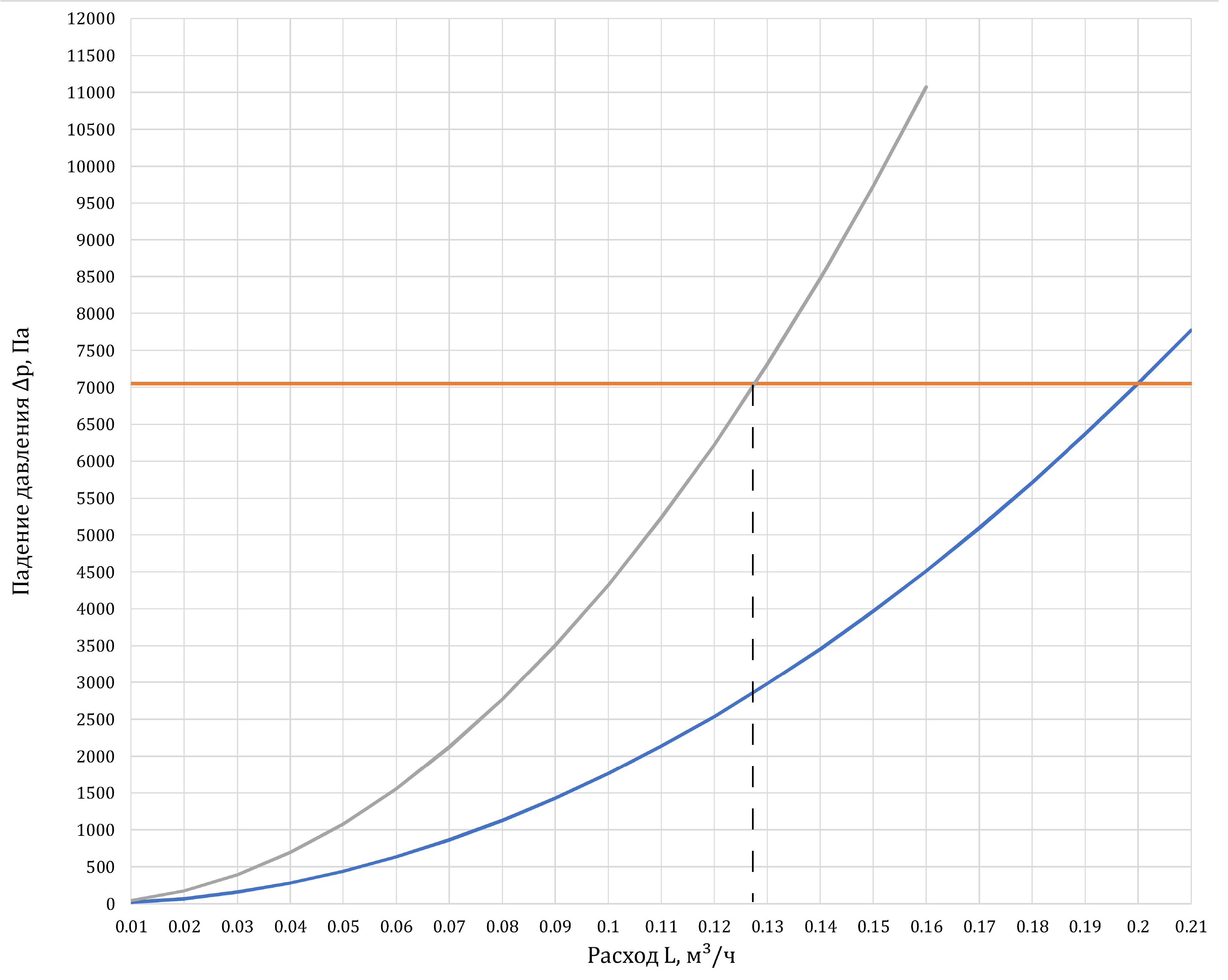
Итак, сопротивления сети когда все радиаторы открыты и когда часть из них закрыта мы посчитали ранее, они составляют \(C_{E1}=176247\) \eqref{eq:6} и \(C_{E2}=432390\) \eqref{eq:7}. Изобразим на графике 4↓ эти уже известные характеристики сети, только теперь для насоса вместо постоянной характеристики нарисуем характеристику поддержания постоянного давления.
Два режима и насос с постоянным перепадом давлений
figure Двухтрубная система отопления - График 3.png
Из графика видно, что теперь расход падает до \(\approx 0.128\) м3/ч, что меньше чем в предыдущем примере, а давление, которое развивает насос, остаётся таким же, как и при открытых радиаторах \(\approx 7100\) Па
Найдём расход в каждом из радиаторов A и B. Общее падение давления в сети после отключения радиаторов C и D будет складываться из падения давления на участке через КОТЁЛ \(\Delta p_{2K1}\) с новым расходом \(L_{E2}\) и через параллельно соединённые участки с радиаторами A и B:
$$\Delta p_{E2}=\Delta p_{2K1}+\Delta p_{1A2}=\Delta p_{2K1}+\Delta p_{13B42}\nonumber$$
Зная сопротивление участка через КОТЁЛ можно легко узнать значение \(\Delta p_{2K1}\) с новым расходом \(L_{E2}\):
$$\Delta p_{2K1}=C_{2K1}\cdot L_{2K1}^{2}=50000\cdot0.128^{2}=820\nonumber$$
Падение давления через параллельно соединённые участки с радиаторами можно найти как разность общего давления на сеть и падение давления на участке через КОТЁЛ:
$$\Delta p_{1A2}=\Delta p_{13B42}=\Delta p_{E}-\Delta p_{2K1}=7100-820=6280\nonumber$$
Так как сопротивление участков 1-A-B и 1-3-B-4-2 разное, расход тоже будет различаться. Найдём расход через радиатор A:
$$L_{1A2}=\sqrt{\frac{\Delta p_{1AB}}{C_{1AB}}=}\sqrt{\frac{6280}{1500000}}\approx0.065\nonumber$$
Тогда расход через радиатор B будет:
$$L_{13B42}=\sqrt{\frac{\Delta p_{13B42}}{C_{13B42}}}=\sqrt{\frac{6280}{1560000}}\approx0.063\nonumber$$
Из этого примера видно, что в случае с насосом регулируемым по перепаду давлений, расход через открытые радиаторы изменится в меньшей степени, хотя и повышение расхода всё равно будет.

Источники


Ганс Роос, "Гидравлика систем водяного отопления"