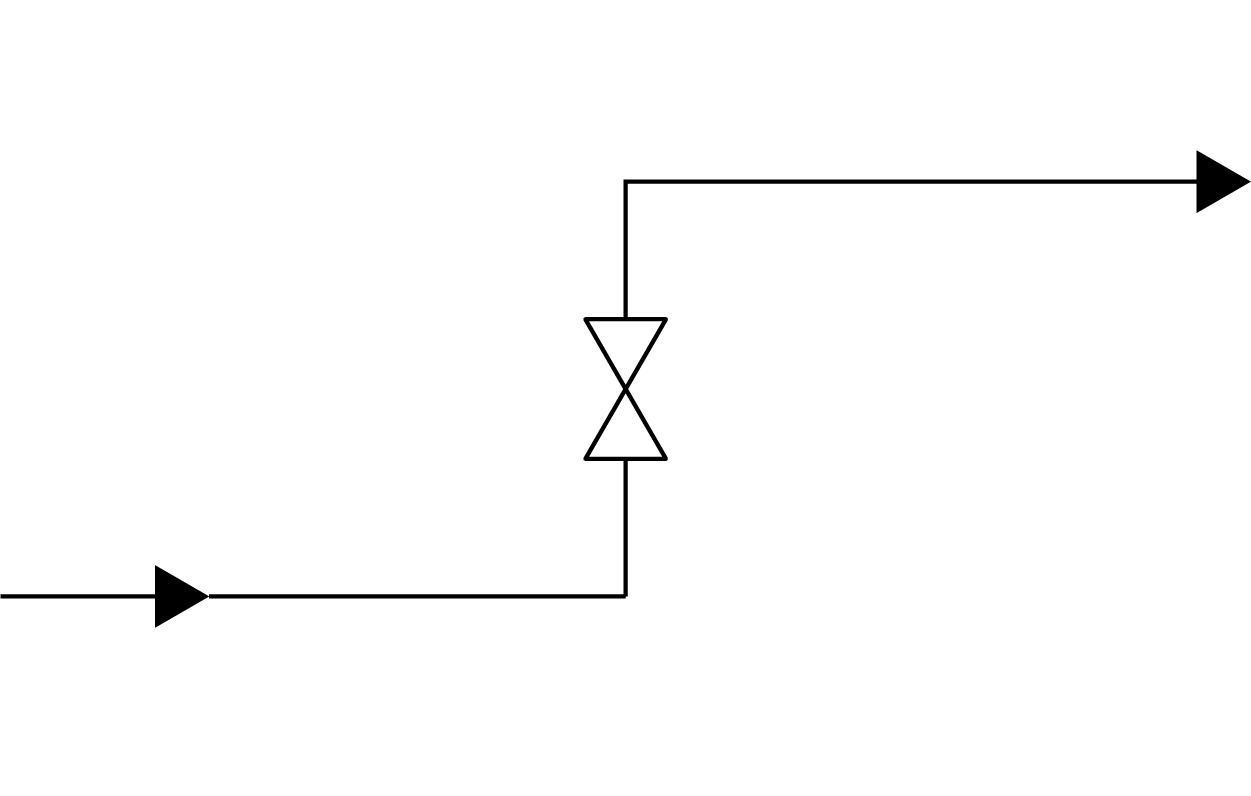Онлайн-расчёты Скачать Статьи-формулы Нормы ОВ Справочник-таблицы Контакты Помощь сайту

Параллельное и последовательное соединение участков

Здесь для объяснения расчёта параллельно или последовательно соединённых участков используется метод характеристик сопротивлений

Обозначения

$\Delta p\quad$ Падение давления$kPa$
$L_{p}\quad$ Общий расход сети через первый и второй участки при параллельном соединении $\frac{m^{3}}{h}$
$x\quad$ Просто переменная "икс"
$a\quad$ Просто переменная "а"
$y\quad$ Просто переменная "игрик"
$C\quad$ Гидравлическое сопротивление
$k_{vs}\quad$ Пропускная способность $\frac{m^{3}}{h\,bar^{0.5}}$
$\zeta\quad$ Коэффициент местного сопротивления "зета"

Единицы измерений обозначены латинскими буквами согласно системе SI

Гидравлическая характеристика сети

Каждая сеть в статическом или постоянном состоянии имеет зависимость падения давления $\Delta p$ в этой сети от расхода жидкости $L$ , который проходит через эту сеть. К примеру какая-то сеть, состоящая из трубы, пары фитингов и регулирующего клапана, как на рисунке 1↓ при определённом расходе будет иметь определённое падения давления. 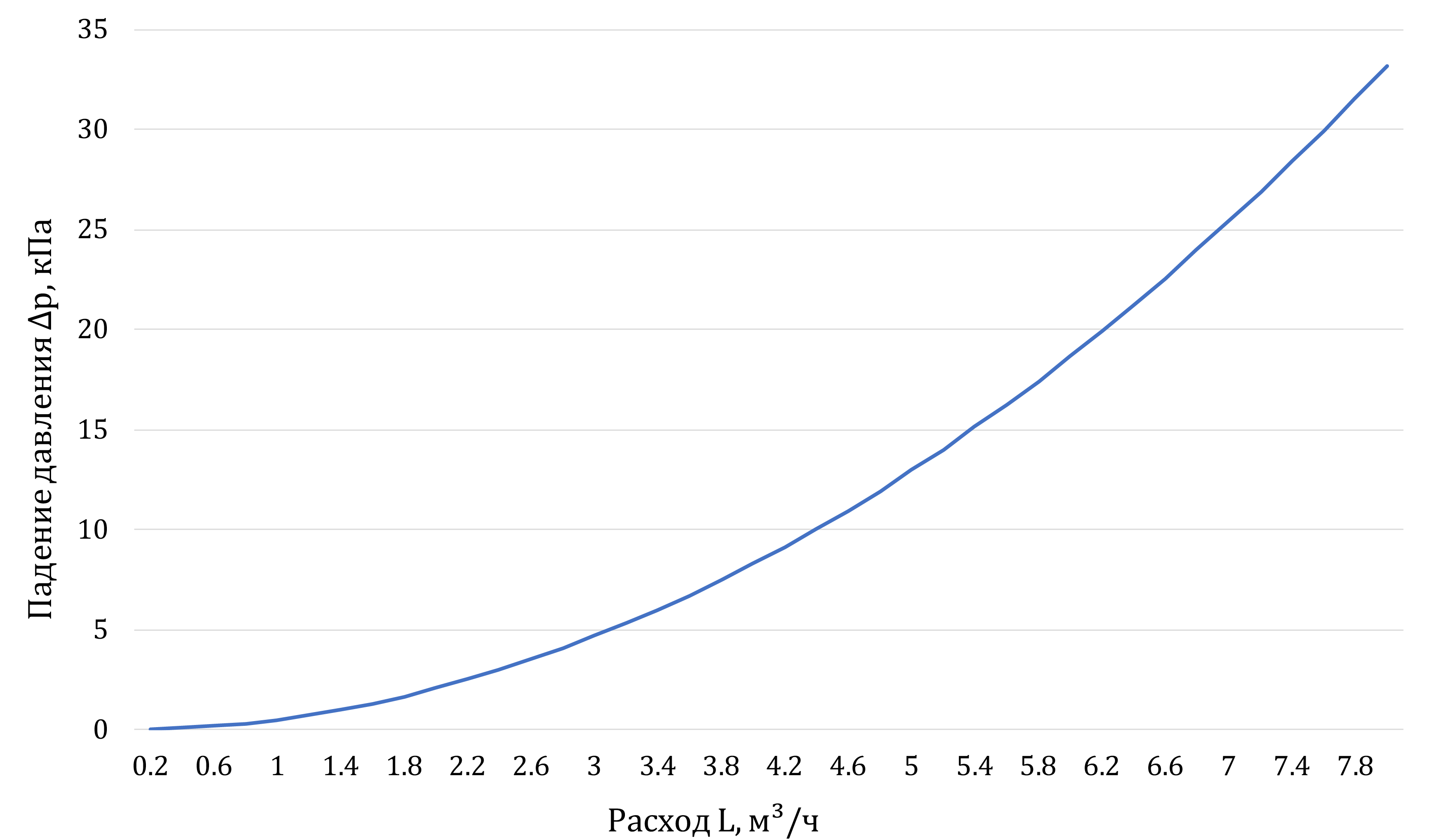При другом расходе падение давления будет другое и так далее, и все эти значения графически будут лежать на одной и той же кривой при условии, что вентиль не закрывается и не открывается 2↓. Если же вентиль поменяет своё положение, скажем немного закроется, то фактически это будет уже другая сеть, и для этой новой сети зависимость падения давления $\Delta p$ от расхода $L$ будут уже другие 3↓. При этом при закрытии вентиля кривая будет проходить круче, а при открытии вентиля - более полого . Эта зависимость и называется характеристикой сети.

Зависимость падения давления $\Delta p$ от расхода $L$ для определённой сети называется характеристикой сети

Рисунок 1 Схема произвольного участка сети

Рисунок 2 Характеристика сети 1

Рисунок 3 Характеристика сети 2

Примечательно, что этот график характеристики сети - вообще-то парабола, имеющая вид $x=a\cdot y^2$ [A] [A] использование показателя степени «2» не совсем верно, но подходит для практической оценки поведения сети. Подробнее об этом в книге Ганс Роос «Гидравлика систем водяного отопления», где

$x$ - падение давления $\Delta p$

$a$ - характеристика гидравлического сопротивления $C$

$y$ - расход $L$

Таким образом, зная гидравлическое сопротивление $C$ можно легко построить график характеристики сети и оценить её поведение при различных режимах работы.

Общая часть

Любое разветвление в сетях является параллельным соединением, а последовательное соединение - это просто соединение участка за участком, фасонного элемента за прямой трубой. Про то, как посчитать гидравлическое сопротивление $C$ и оценить работу сети подробно описано на странице поведение двухтрубной системы отопления. Здесь же посмотрим, как построить характеристики параллельно и последовательно соединённых участков

Параллельно соединённые участки

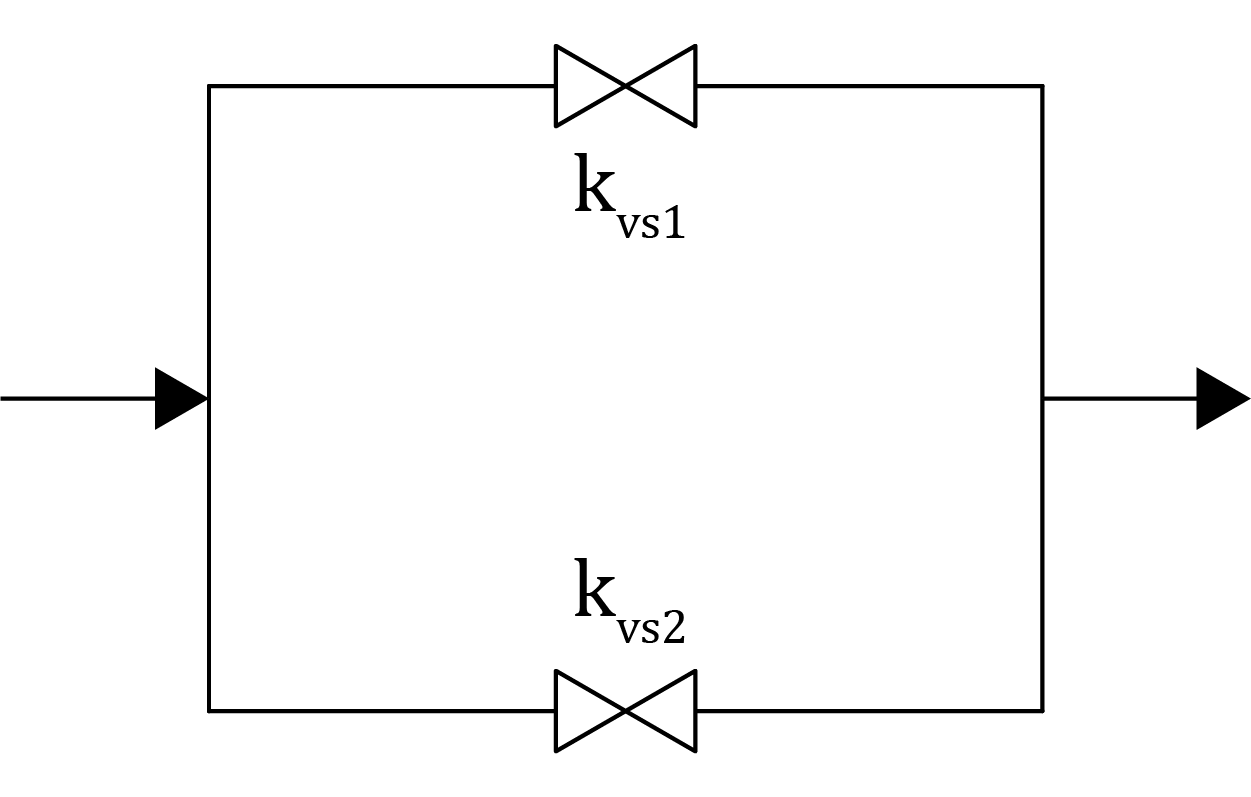
Схема параллельного соединения двух участков показана на рисунке 4↓. Допустим, что каждое ответвление состоит из:

двух участков трубы Ø50 длиной 10 метров
вентиля пропускной способностью $k_{vs}=16$
двух отводов 90° Ø50

Гидравлическое сопротивление $C$ для каждого элемента можно посчитать по формулам со страницы гидравлический расчёт методом характеристик сопротивления:

Труба $l\cdot\lambda\cdot\frac{0.6173\cdot\rho}{\pi^{2}\cdot d^{5}}\approx10\cdot0.028\cdot\frac{0.6173\cdot1000}{10^{6}\cdot3.142^{2}\cdot0.05^{5}}=55$

Отвод $\zeta\cdot\frac{0.6173\cdot\rho}{10^{6}\cdot\pi^{2}\cdot d^{4}}\approx0.5\cdot\frac{0.6173\cdot1000}{10^{6}\cdot3.142^{2}\cdot d^{4}}=5$

Вентиль $\frac{10^{5}}{k_{vs}^{2}}=\frac{10^{5}}{16^{2}}\approx390.6$

Значения параметров без особых подробностей показаны в таблице 1↓

Таблица 1 Параметры элементов при параллельном соединении

Элемент	Расход $L_{1}$	Длина $l$	КМС$\zeta$	$k_{vs}$	$C$
Труба	5	10	-	-	55
Отвод	5	-	0.5	-	5
Вентиль	5	-	- [B] [B] вентиль является местным сопротивлением и у него есть значение $\zeta$, но в этом расчёте нас больше интересует показатель $C$	16	390.6

Теперь, зная значения гидравлического сопротивления $C$ каждого элемента, можно посчитать общее гидравлическое сопротивление одной ветви. Так как элементы соединены последовательно, [C] [C] то есть друг за другом их эквивалентное гидравлическое сопротивление $C_{Es}$ будет суммой гидравлических сопротивлений каждого элемента:

$$C_{E1}=\sum C_{i}\label{eq:1}$$

$$C_{E1}=2\cdot55+2\cdot5+390.6=510.6$$

а эквивалентное гидравлическое сопротивление всей сети $C_{Ep}$ [D] [D] индекс $p$ означает «parallel» - «параллельный» из двух ветвей можно посчитать по формуле:

$$C_{Ep}=\frac{C_{1}\cdot C_{2}}{C_{1}+C_{2}+2\cdot\sqrt{C_{1}\cdot C_{2}}}\label{eq:2}$$

в итоге получится:

$$C_{Ep}=\frac{510.6\cdot510.6}{510.6+510.6+2\cdot\sqrt{510.6\cdot510.6}}\approx127.7$$

тогда характеристика сети будет представлена параболой:

$$\Delta p=C_{Ep}\cdot L^{2}$$

учитывая то, что при параллельном соединении участков падение давления $\Delta p$ будет одинаково для первого и второго участка [E] [E] по-другому быть не может: в точках соединения ветвей возможно только одно значение давления, так как точка одна, а расход через два участка $L_{p}$ будет суммой расходов $L_{1}+L_{2}$, можно сделать вывод, что при графическом построении эквивалентной характеристики будут складываться расходы при одинаковом давлении

при параллельном соединении участков графически эквивалентную характеристику можно построить сложив расходы при одинаковом давлении

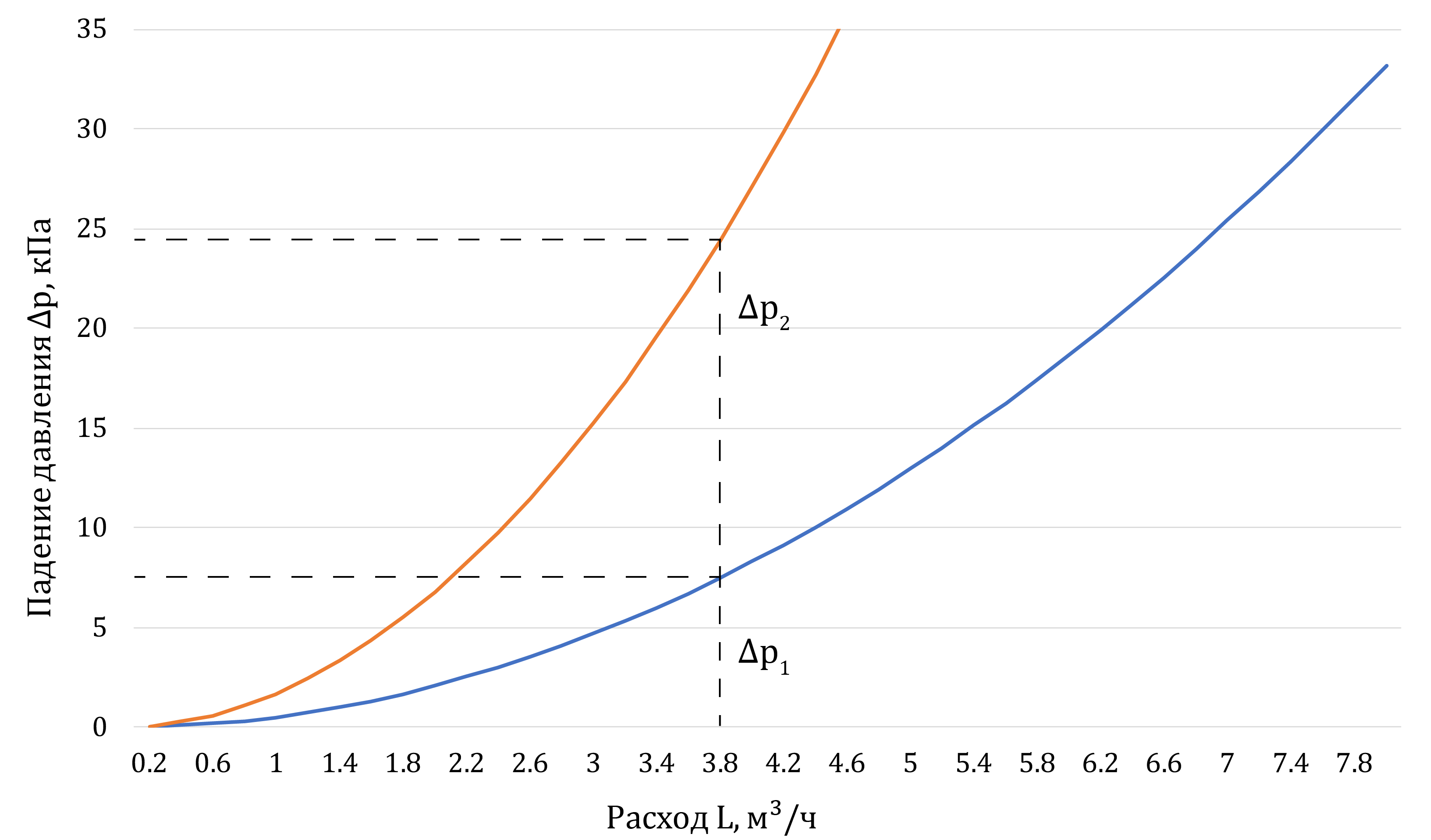
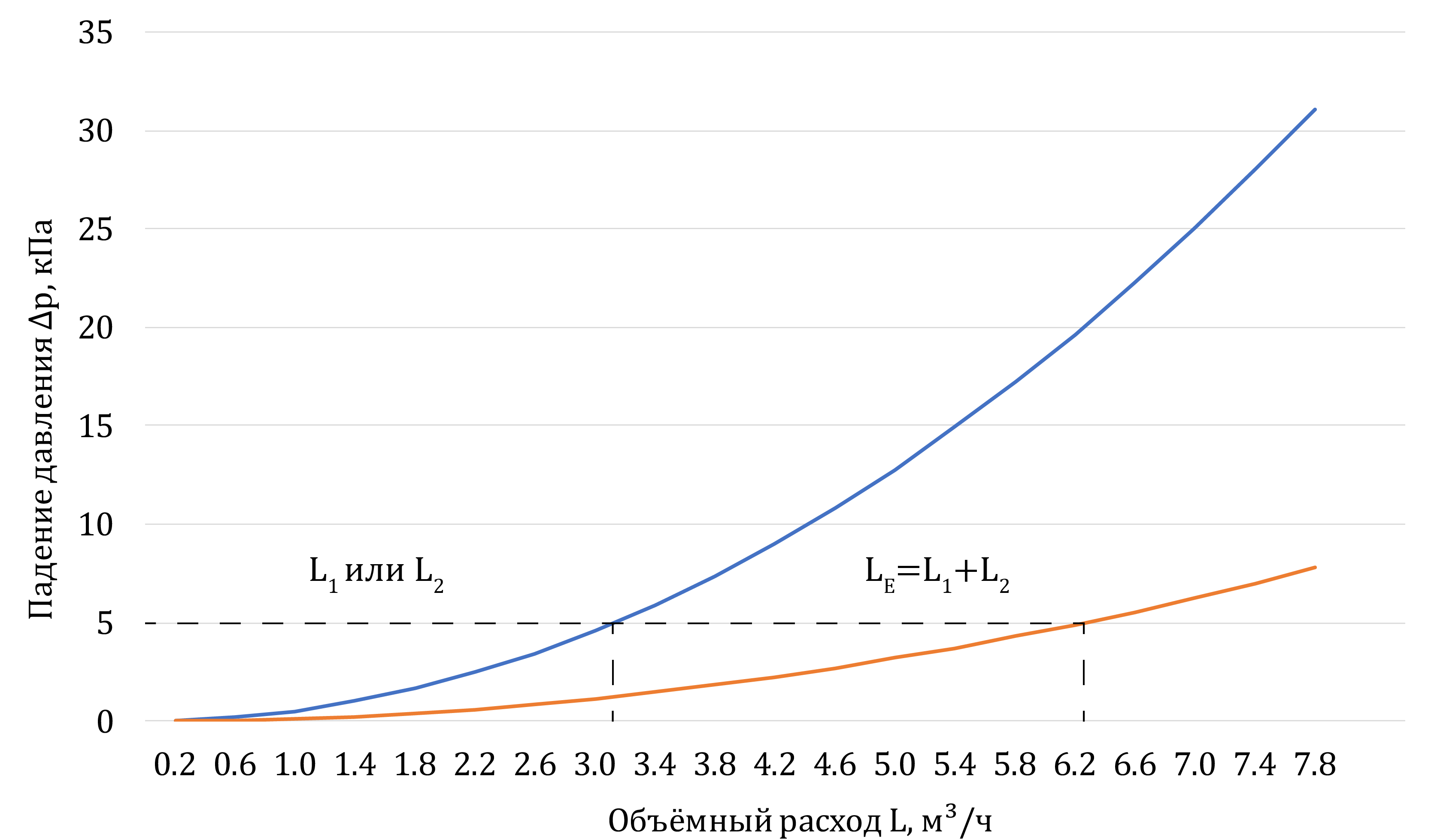
График характеристики сети для одного из параллельных участков изображён на рисунке 2↑. Для всей сети из двух параллельных участков - на рисунке 5↓. Как видно, характеристика всей сети строится путём сложения расходов отдельных участков при одинаковом давлении, и очевидно:

при параллельном соединении характеристика всей сети проходит более полого, чем характеристики отдельных участков

Рисунок 4 Параллельные участки

Рисунок 5 Характеристика сети из двух параллельных участков

figure Характеристика 3 - параллельное соединение.png

Последовательно соединённые участки

По смыслу последовательное соединение участков не равнозначно их параллельному соединению, так как параллельное соединение - это разветвление сети, что является обычным делом в любой системе отопления или охлаждения, а последовательное соединение - это просто соединение элементов друг за другом, то есть какая-либо одна ветвь например. Поэтому правильнее говорить не о последовательном соединении участков, а скорее о последовательном соединении элементов.

При последовательном соединении эквивалентное гидравлическое сопротивление $C_{Es}$ [F] [F] индекс «s» означает «serial» - «последовательный» будет равно сумме гидравлических сопротивлений $C$ отдельных элементов

вычисляется по формуле 1↑, повторим её ещё раз:

$$C_{Ep}=\sum C_{i}$$

Чем выше гидравлическое сопротивление $C$, тем круче проходит характеристика сети

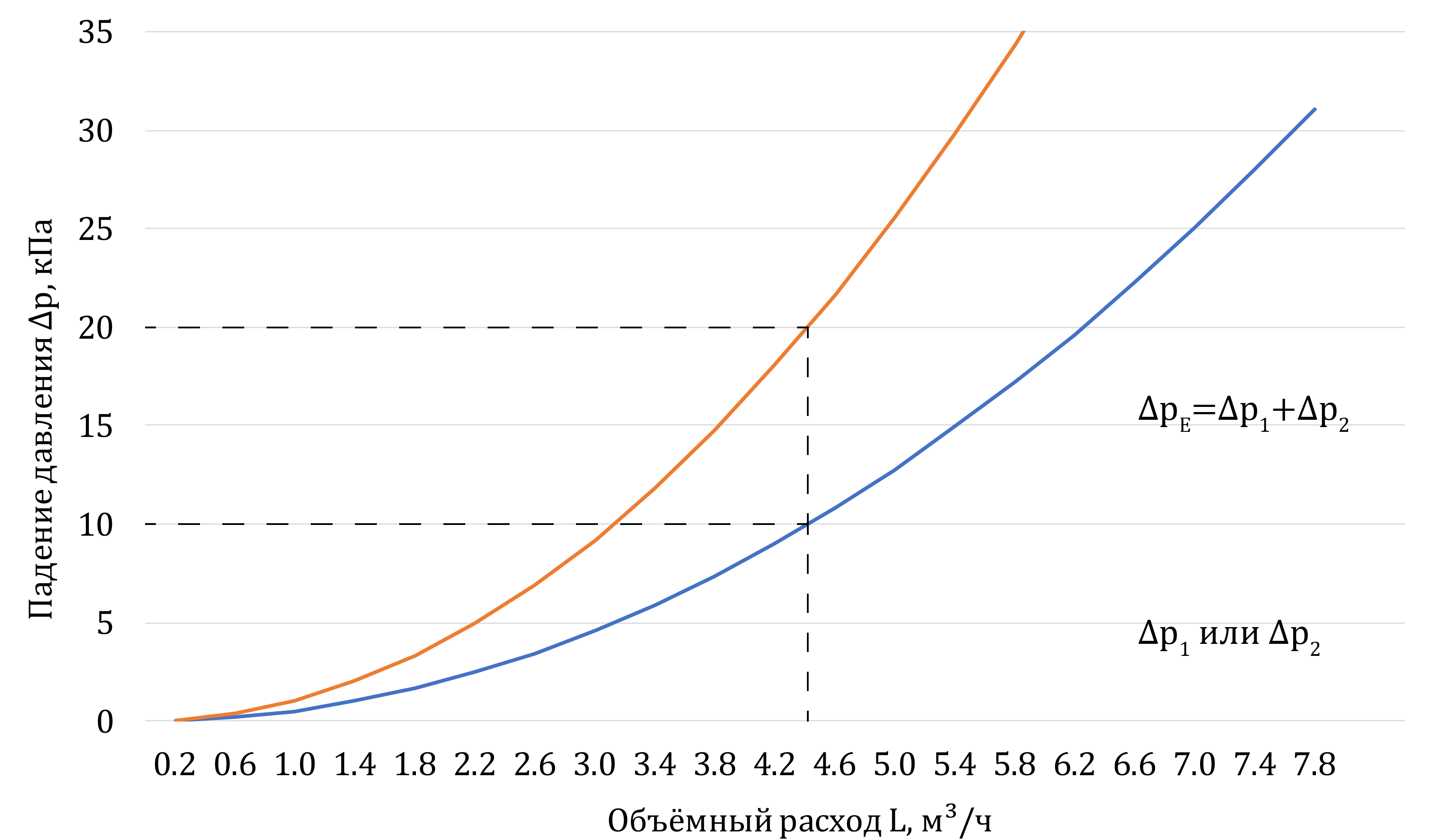
Если представить, что нам зачем-то понадобилось изобразить графически эквивалентную характеристику двух участков с параметрами из таблицы 1↑, соединённых последовательно [G] [G] на практике конечно это маловероятно - обычно просто вычисляются гидравлические сопротивления $C$ всех элементов и складываются, чтобы узнать общее гидравлическое сопротивление ветви, то в этом случае будут складываться падения давлений $\Delta p$ при одинаковых расходах $L$ - так, как на рисунке 6↓

Рисунок 6 Характеристика сети из двух последовательных участков

figure Характеристика 4 - последовательные участки.png

Советы и рекомендации

Практическое применение В России вероятно более распространён метод расчёта по удельным потерям давления по длине, хотя расчёт с использованием гидравлических сопротивлений также давно известен и описан например в книгах под редакцией И.Г.Староверова «Внутренние санитарно-технические устройства. Часть 1. Отопление» или А.Н.Сканави «Отопление». Приемущество этого метода в том, что с его помощью можно оценить поведение системы в динамическом режиме, например когда в двухтрубной системе отопления закрывается часть приборов.

Источники

[1] Роос «Гидравлика систем водяного отопления»

Элемент	Расход \(L_{1}\)	Длина \(l\)	КМС\(\zeta\)	\(k_{vs}\)	\(C\)
Труба	5	10	-	-	55
Отвод	5	-	0.5	-	5
Вентиль	5	-	- [B] [B] вентиль является местным сопротивлением и у него есть значение \(\zeta\), но в этом расчёте нас больше интересует показатель \(C\)	16	390.6