Онлайн-расчёты Скачать Статьи-формулы Нормы ОВ Справочник-таблицы Контакты

Вопросы, связанные с авторскими правами Производителям оборудования

Понятие производной для начинающих

Движение, путь и скорость

Рассмотрим поступательное движение тела вдоль некоторой прямой линии; расстояние определённой точки тела от определённой точки на этой прямой обозначим $z$, причём в одну сторону это расстояние будем считать положительным, а в другую - отрицательным. Пусть, например, прямая, вдоль которой движется тело, расположена вертикально, точки выше 0 соответствуют положительным $z$, точки ниже 0 - отрицательным $z$.

При движении координата $z$ зависит от времени (мы будем сокращённо говорить: "координата $z$" вместо "расстояние определённой точки тела от определённой точки на прямой"). Движение тела определяется зависимостью $z$ от времени $t$, т.е. заданием функции $z(t)$. Зная функцию $z(t)$, можно найти положение тела в любой момент времени.

Функцию $z(t)$ можно изобразить графически, откладывая по оси абсцисс время (ось t), а по оси ординат - величину $z$, характеризующую положение тела.

При равномерном движении с постоянной скоростью $v$ путь $z$, пройденный за время $t$, равен произведению $z=v\cdot t$. Обозначим $z_{0}$ координату тела в момент $t=0$. Путь, пройденный за время $t$, равен разности $z(t)-z_{0}$. Значит,

$$z(t)=z_{0}+v\cdot t\label{eq:1}$$

Следовательно, при равномерном движении зависимость координаты от времени даётся линейной функцией. График зависимости $z(t)$ при равномерном движении представляет собой прямую линию на координатной плоскости, у которой по оси абсцисс (горизонтальной) отложено время $t$, а по оси ординат (вертикальной) отложена координата $z$

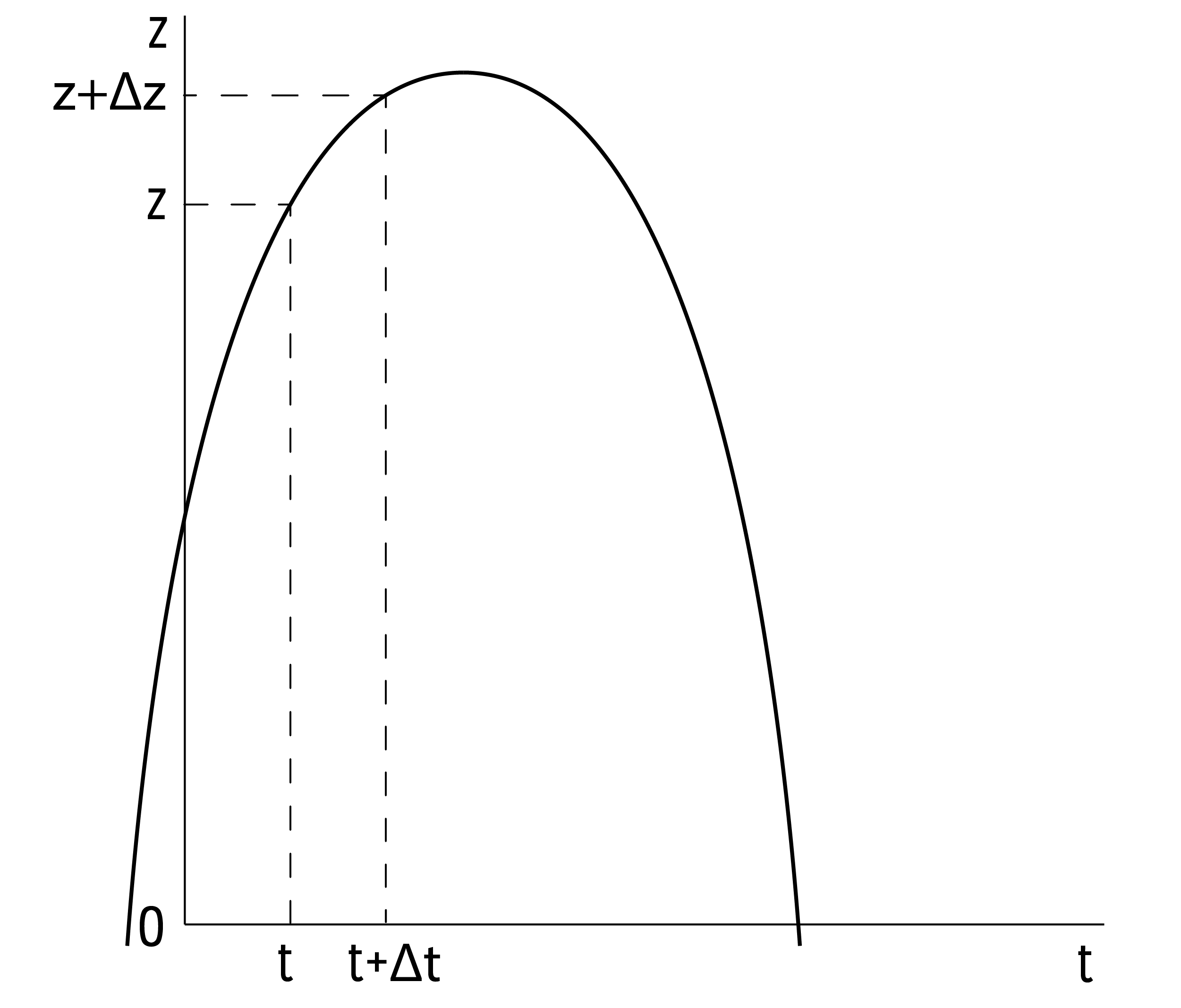
Если же тело движется неравномерно, зависимость $z(t)$ выражается более сложными формулами и соответствующий график представляет собой ту или иную кривую

Разберём подробно следующую задачу: задана функция $z(t)$, т.е. зависимость координаты тела от времени, нужно найти скорость движения тела $v$. В общем случае неравномерного движения скорость не остаётся постоянной, она меняется с течением времени. Значит, скорость $v$ есть также функция времени $v(t)$, и задача заключается в том, чтобы выразить $v(t)$ через известную функцию $z(t)$.

В частном случае равномерного движения (с постоянной скоростью) всё просто. Скорость определяется как путь, пройденный за единицу времени. Так как скорость постоянна, то безразлично, какой именно участок пути и какой промежуток времени выбран для определения скорости.

Найдём путь, пройденный за одну секунду от момента $t_{1}$ секунд до момента $t_{1}+1$ секунд. Этот путь равен разности координат $z(t_{1}+1)$ и $z(t_{1})$:

$$z(t_{1}+1)-z(t_{1})=[z_{0}+v\cdot(t_{1}+1)]-[z_{0}+v\cdot t_{1}]=v\nonumber$$

и численно оказался равным скорости. Можно взять произвольный промежуток времени между $t_{1}$ и $t_{2}$ и разделить пройденный путь $z_{2}-z_{1}$ на величину промежутка $t_{2}-t_{1}$:

$$t_{2}-t_{1}\label{eq:2}$$

Именно потому, что скорость постоянна, мы могли выбирать для её вычисления любой интервал $t_{2}-t_{1}$, и ответ не зависел ни от момента $t_{1}$, ни от величины этого интервала. В общем случае движения с переменной скоростью это уже не так.

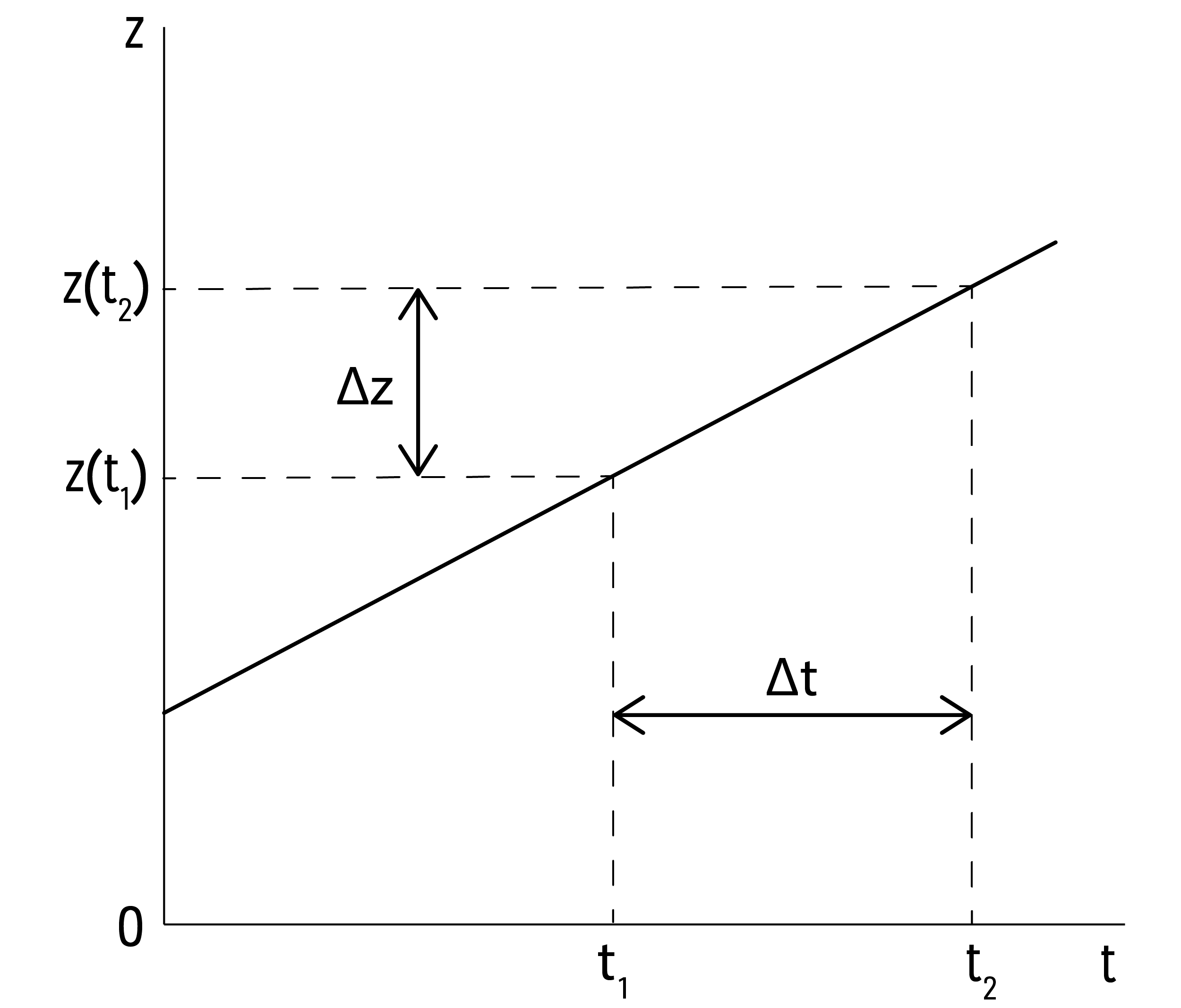
Прежде чем переходить к более общему случаю удобно переменить обозначения. Назовём $t_{1}=t$, $t_{2}=t+\Delta t$, так что разность $t_{2}-t_{1}$, т.е. промежуток времени, обозначена $\Delta t$ 1↓. Подобно этому обозначим $\Delta z$ разность

$$z(t_{2})-z(t_{1})=z(t+\Delta t)-z(t)=\Delta z\nonumber$$

В этих обозначениях средняя скорость $v_{\text{ср}}$ в интервале $\Delta t$ от $t$ до $t+\Delta t$ равна [A] [A] Отметим, что $\Delta$ - это не множитель, а знак, заменяющий слово «приращение», так что сокращать $\Delta$ в числителе и знаменателе дроби нельзя. Сам знак $\Delta$ - это прописная буква «дельта» греческого алфавита, так что $\Delta t$ читается «дельта тэ», $\Delta z$ - «дельта зэт»; часто читают $\Delta t$ - «приращение времени», $\Delta z$ - «приращение пути».

$$v_{\text{ср}}=\frac{\Delta z}{\Delta t}\label{eq:3}$$

Мы говорим здесь о средней скорости потому, что общем случае сама скорость может меняться на протяжении интервала $\Delta t$.

Рассмотрим второй пример, когда $z(t)$ задаётся формулой

$$z(t)=z_{0}+bt+ct^{2}\label{eq:4}$$

На рис. 2↓ приведён один из возможных графиков, отвечающих функции вида 4↑.

Рисунок 1

figure Понятие производной для начинающих - график 1.png

Рисунок 2

figure Понятие производной для начинающих - график 2.png

Вычислим среднюю скорость $v_{\text{ср}}$ на интервале $\Delta t$ по формуле 3↑. Для этого запишем:

$$z(t)=z_{0}+bt+ct^{2}\nonumber$$

$$z(t+\Delta t)=z_{0}+b(t+\Delta t)+c(t+\Delta t)^{2}\nonumber$$

$$\Delta z=z(t+\Delta t)-z(t)=b\Delta t+2ct\Delta t+c(\Delta t)^{2}\nonumber$$

Отсюда получается

$$v_{\text{ср}}=\frac{\Delta z}{\Delta t}=b+2ct+c\Delta5\label{eq:5}$$

Сравним результаты 2↑ и 5↑ для средней скорости при движении по закону 1↑ и по закону 4↑. Второй пример отличается тем, что в нём средняя скорость зависит и от самого момента $t$, и от промежутка времени $\Delta t$.

Как же найти мгновенную скорость?

Скорость меняется постепенно, поэтому чем меньше промежуток времени, в течение которого производится измерение пройденного пути, тем меньше успеет измениться скорость, тем ближе будет средняя скорость к её мгновенному значению.

В формуле 5↑ $v_{\text{ср}}$ содержит два члена, не зависящих от величины промежутка $\Delta t$, и один член, пропорциональный $\Delta t$. При очень маленьких $\Delta t$ этим членом можно пренебречь, а $v_{\text{ср}}$ при этом даёт величину мгновенной скорости

$$v_{\text{мгн}}=b+2ct\label{eq:6}$$

Внимательный читатель, вероятно, уже узнал в выражениях 4↑ и 6↑ известные из школьного учебника физики формулы для равноускоренного движения:

$$\begin{cases} z(t)=z_{0}+v_{0}t+\frac{at^{2}}{2}\\ v(t)=v_{0}t+at \end{cases}\label{eq:7}$$

Для этого нужно лишь вместо $b$ подставить $v_{0}$ - начальную скорость (т.е. скорость в момент $t=0$), а вместо $c$ подставить $a/2$, где $a$ - ускорение.

Мы вычислили мгновенную скорость в момент $t$, исходя из средней скорости в промежутке от $t$ до $t+\Delta t$. Попробуем теперь вычислить её, выбирая промежуток несколько по-иному. Найдём среднюю скорость в промежутке от $t_{1}=t-3\Delta t/4$ до $t_{2}=t+\Delta t/4$; длительность промежутка по-прежнему равна $t_{2}-t_{1}=\Delta t$. Из формулы 4↑ получим

$$z(t_{1})=z_{0}+b(t-\frac{3\Delta t}{4})+c(t-\frac{3\Delta t}{4})^{2}\nonumber$$

$$z(t_{2})=z_{0}+b(t+\frac{\Delta t}{4})+c(t+\frac{\Delta t}{4})^{2}\nonumber$$

$$z(t_{2})-z(t_{1})=b\Delta t+2ct\Delta t-\frac{1}{2}c(\Delta t)^{2}\nonumber$$

Отсюда следует, что

$$v_{\text{ср}}=\frac{z(t_{2})-z(t_{1})}{t_{2}-t_{1}}=b+2ct-\frac{1}{2}c\Delta t\label{eq:8}$$

Если сравнить формулы 5↑ и 8↑, то видно, что средние скорости на интервале от $t$ до $\Delta t$ и на интервале от $t-3\Delta t/4$ до $t+\Delta t/4$ отличаются на величину $c\Delta t[1-(-1/2)]=3c\Delta/2$. Но если мы хотим найти мгновенную скорость, то нужно брать очень маленький интервал $\Delta t$; при этом различие пропадает, и мы снова получаем для мгновенной скорости $v_{\text{мгн}}=b+2ct$.

Мы рассмотрели понятие мгновенной скорости для двух конкретных примеров: для равномерного и для равноускоренного движения. В следующем параграфе мы дадим более точное определение мгновенной скорости при произвольном законе движения.

Производная функции - предел отношения приращений

В предыдущем параграфе в связи с задачей о мгновенной скорости мы пришли к рассмотрению отношений вида

$$\frac{z(t_{2})-z(t_{1})}{t_{2}-t_{1}}\nonumber$$

при очень близких между собой значениях $t_{2}$ и $t_{1}$.

Выражение «очень близкие» является неопределённым, нестрогим. Точная формулировка такова: необходимо найти предел, к которому стремится отношение

$$\frac{z(t_{2})-z(t_{1})}{t_{2}-t_{1}}\label{eq:9}$$

при $t_{2}$, стремящимся к $t_{1}$. Используя обозначения $\Delta t$ и $\Delta z$, это отношение можно переписать в виде

$$v_{\text{ср}}=\frac{\Delta z}{\Delta t}\label{eq:10}$$

В формуле 10↑ величины $\Delta t$ и $\Delta z$ зависимы: можно выбрать любой промежуток времени $\Delta t$, но после того, как промежуток времени $\Delta t$, стоящий в знаменателе, выбран, подразумевается, что $\Delta z$ в числителе - не любой отрезок пути, а именно тот, который соответствует промежутку времени $\Delta t$. В формуле 9↑ это было очевидно из самого написания аргументов функции $z(t_{2})$, $z(t_{1})$ в числителе, формула 10↑ есть просто другая запись формулы 9↑.

Интересующая нас величина мгновенной скорости $v(t)$ в момент времени $t$ есть предел отношения $\frac{\Delta z}{\Delta t}$ при $\Delta t$, стремящемся к нулю. Очевидно, стремление $\Delta t$ к нулю равносильно стремлению $t_{2}$ к $t_{1}$, поскольку $\Delta t=t_{2}-t_{1}$. Приведённая формулировка записывается так:

$$v(t)=\lim_{\Delta t\rightarrow0}(\frac{\Delta z}{\Delta t})\nonumber$$

Буквы lim [B] [B] начальные буквы латинского слова «limes» - «лимес» - «предел» обозначают «предел»; внизу записано, о каком именно пределе идёт речь - при $\Delta t$, стремящемся к нулю, стрелка заменяет слово «стремится», в скобках указана та величина $\frac{\Delta z}{\Delta t}$, предел который ищется.

Что значит «предел», «стремление к пределу»? Те расчёты, которые мы производили в предыдущем параграфе, как раз и служили наглядным пояснением этих понятий. Мы видели, что при малых промежутках $\Delta t$ величина $v_{\text{ср}}$ во втором примере отличалась от значения $v_{\text{мгн}}$ на малую величину, пропорциональную $\Delta t$. Хотя коэффициент пропорциональности при $\Delta t$ мог быть различным при разных способах выбора интервала, для малых значений $\Delta t$ в выражении для $v_{\text{ср}}$ мы всегда могли пренебречь членом с $\Delta t$.

Итак, отношение

$$\frac{\Delta z}{\Delta t}=\frac{z(t_{2})-z(t_{1})}{t_{2}-t_{1}}\nonumber$$

стремится к определённому пределу, когда $\Delta t=t_{2}-t_{1}$ стремится к нулю; при $\Delta t$, стремящемся к нулю, $t_{2}$ и $t_{1}$ неограниченно сближаются между собой, и общую их величину мы обозначаем (когда $\Delta t\rightarrow0$) $t_{2}=t_{1}=t$.

Предел отношения, т.е. мгновенная скорость $v$, есть определённая функция $t$,

$$\lim_{\Delta t\rightarrow0}\frac{\Delta z}{\Delta t}=v(t)\nonumber$$

Почему при вычислении скорости по заданной формуле $z(t)$ приходится проводить такой длинный расчёт, находить $\Delta z$ для различных $\Delta t$ и затем только находить предел $\lim_{\Delta t\rightarrow0}\frac{\Delta z}{\Delta t}$? Нельзя ли сразу взять значение $\Delta t=0$? При этом мы получили бы $\Delta z=0$, так как $\Delta t=t_{2}-t_{1}$, и если $t_{2}=t_{1}$, то и $z(t_{2})=z(t_{1})$ и $\Delta z=z(t_{2})-z(t_{1})=0$. Значит, при таком бездумном способе действий мы получили бы $\frac{\Delta z}{\Delta t}=\frac{0}{0}$, т.е. не получили бы никакого определённого ответа.

При вычислении скорости вся суть заключается в том, чтобы брать малые $\Delta t$ и соответствующие им малые $\Delta z$. При этом получается каждый раз вполне определённое отношение $\frac{\Delta z}{\Delta t}$; когда $\Delta t$ уменьшается, стремится к нулю, то $\Delta z$ уменьшается приблизительно пропорционально величине $\Delta t$, а поэтому отношение остаётся приблизительно постоянным.

Отношение $\frac{\Delta z}{\Delta t}$ стремится к определённому пределу при стремлении $\Delta t$ к нулю.

Величина этого предела - мгновенная скорость $v(t)$ в случае движения или в общем случае производная функции $z(t)$ - зависит от вида функции $z(t)$ и от значения переменной $t$. В следующем параграфе мы проведём алгебраически вычисление производной нескольких простейших функций и для них найдём точное значение предела, т.е. производной.

Обозначения производной. Производная степенной функции

Предел отношения приращения функции к приращению независимой переменной при стремлении к нулю приращения независимой переменной имеет первостепенное значение и для высшей математики и для её приложений: выше мы видели, например, что такое важнейшее понятие, как мгновенная скорость движения, находится именно с помощью предела такого отношения. Поэтому предел этого отношения имеет специальное название: производная функция или короче производная. Первое название связано с тем, что если $z$ есть функция $t$, $z(t)$, то и предел отношения $\lim_{\Delta t\rightarrow0}\frac{\Delta z}{\Delta t}=v$ также есть функция (другая) $v(t)$ переменной $t$ - зависит от значения $t$, к которому стремятся $t_{1}$ и $t_{2}$, или, как иначе говорят, $v$ зависит от значения $t$, «при котором берётся производная $z$».

Для производной имеются специальные обозначения.

Один способ обозначения:

$$\frac{\partial z}{\partial t}=\lim_{\Delta t\rightarrow0}\frac{\Delta z}{\Delta t}\nonumber$$ $$\frac{\partial T}{\partial x}=\lim_{\Delta x\rightarrow0}\frac{\Delta T}{\Delta x}\nonumber$$

При этом величина $\frac{\partial z}{\partial t}$ [C] [C] читается: «дэ-зэт по дэ-тэ» рассматривается на как дробь, а просто как сокращённая запись предела, стоящего справа. Величина $\frac{\partial z}{\partial t}$ записана в форме дроби для того, чтобы напоминать, что эта величина получена из дроби $\frac{\Delta z}{\Delta t}$ путём перехода к пределу.

Обратите внимание, что

$$\frac{\partial z}{\partial t}\nonumber$$

не одно и то же, что

$$\frac{\Delta z}{\Delta t}\nonumber$$

Источники

[ 1] Я.Б.Зельдович «Высшая математика для начинающих»